Suku Banyak

Suku banyak atau polinominal merupakan pernyataan matematika yang melibatkan penjumlahan perkalian pangkat dalam satu atau lebih variable dengan koefisien. Bisa dibilang polinominal merupakan bentuk aljabar dengan pangkat peubah bilangan bulat positif. Suku banyak dalam x berderajat n mempunyai bentuk umum:
dan
adalah konstanta real
koefisien
koefisien
koefisien
dan seterusnya
disebut suku tetap
- n bilangan cacah yang menyatakan derajat suku banyak
NILAI SUKU BANYAK
Suku banyak dalam x berderajat n dapat ditulis dalam bentuk fungsi sebagai berikut:
Nilai  untuk
untuk  adalah
adalah 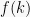 . Nilainya dapat ditentukan dengan dua strategi, yaitu:
. Nilainya dapat ditentukan dengan dua strategi, yaitu:
Substitusi
Misalkan nilai 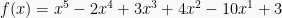 untuk
untuk  dengan
dengan  dapat ditentukan dengan mensubstitusi menjadi:
dapat ditentukan dengan mensubstitusi menjadi:


Skema (bagan)
Misalkan 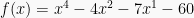 untuk
untuk  . Yang pertama dilakukan adalah mengurutkan penulisan kiri ke kanan mulai dari pangkat tertinggi. Yang ditulis dalam bagan adalah koefisien dari masing-masing derajat suku banyak.
. Yang pertama dilakukan adalah mengurutkan penulisan kiri ke kanan mulai dari pangkat tertinggi. Yang ditulis dalam bagan adalah koefisien dari masing-masing derajat suku banyak.

Tanda(“↓”) menunjukan penjumlahan baris 1 dan baris 2 yang menghasilkan baris hasil. Tanda (“ ”) menunjukan perkalian baris hasil dengan
”) menunjukan perkalian baris hasil dengan  dan menghasilkan baris 2. Dari cara ini diperoleh
dan menghasilkan baris 2. Dari cara ini diperoleh 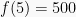 .
.
 ”) menunjukan perkalian baris hasil dengan
”) menunjukan perkalian baris hasil dengan Jika  dan
dan 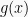 berturut-turut adalah suku banyak berderajat m dan n, dengan
berturut-turut adalah suku banyak berderajat m dan n, dengan  maka operasinya:
maka operasinya:
mempunyai derajat maksimum m
mempunyai derajat
PEMBAGIAN SUKU BANYAK
Misalkan  dibagi dengan
dibagi dengan  memberikan hasil bagi
memberikan hasil bagi  dan sisa pembagian S, diperoleh hubungan:
dan sisa pembagian S, diperoleh hubungan:
Untuk mendapat hasil bagi  dan sisa S digunakan 2 metode yaitu:
dan sisa S digunakan 2 metode yaitu:
Pembagian Bersusun
Pembagian dengan cara bersusun (biasa) sebagai berikut:

Pembagian Sintetik (Horner)
Pembagian dengan cara ini menggunakan bagan seperti berikut:

Berdasarkan kedua penyelesaian tersebut, didapat hasil pembagian 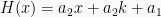 dan sisa pembagian
dan sisa pembagian  .
.
Pembagian dengan 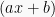
Misalkan 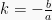 , sehingga bentuk
, sehingga bentuk  menjadi
menjadi 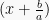 . Jika suku banyak
. Jika suku banyak  dibagi dengan
dibagi dengan 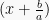 memberikan hasil
memberikan hasil  dan sisa S, maka terdapat hubungan:
dan sisa S, maka terdapat hubungan:
Dengan demikian  dibagi dengan
dibagi dengan 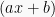 memberikan hasil bagi
memberikan hasil bagi  dan sisa S. Koefisien-koefisien
dan sisa S. Koefisien-koefisien  dan S ditentukan dengan dua jenis cara pembagian sebelumnya dengan mengganti
dan S ditentukan dengan dua jenis cara pembagian sebelumnya dengan mengganti  .
.
Pembagian dengan 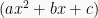
Pembagian suku banyak  oleh pembagi dalam bentuk
oleh pembagi dalam bentuk 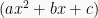 yang tidak bisa difaktorkan, dapat dilakukan dengan metode pembagian bersusun. Sedangkan jika pembagi dapat difaktorkan, penyelesaian dapat dilakukan dengan metode horner. Bentuk umum pembagian ini:
yang tidak bisa difaktorkan, dapat dilakukan dengan metode pembagian bersusun. Sedangkan jika pembagi dapat difaktorkan, penyelesaian dapat dilakukan dengan metode horner. Bentuk umum pembagian ini:
Misalkan 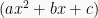 dapat difaktorkan menjadi
dapat difaktorkan menjadi  dan
dan  sehingga
sehingga 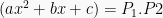 , maka:
, maka:
Langkah-langkah penyelesaiannya adalah:
- Melakukan pembagian suku banyak
oleh
dengan hasil
dan sisanya
.
- Kemudian melakukan pembagian
oleh
dengan hasil
dan sisanya
.
- Hasil bagi
oleh
adalah
sedangkan sisanya
. Ingat jika
atau
membentuk
, perlu untuk membagi
atau
dengan a untuk mendapatkan hasil baginya.
TEOREMA SISA
Misalkan  dibagi
dibagi  dengan hasil bagi
dengan hasil bagi  dan sisa
dan sisa  , maka diperoleh hubungan:
, maka diperoleh hubungan:
Jika  berderajat n dan
berderajat n dan  pembagi berderajat m, dengan
pembagi berderajat m, dengan 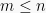 , maka:
, maka:
berderajat
berderajat maksimum
Teorema untuk sisa adalah:
- Jika
berderajat n dibagi dengan
maka sisanya
. Sisa
adalah nilai suku banyak untuk
.
- Jika
berderajat n dibagi dengan
maka sisanya
. Sisa
adalah nilai untuk
.
- Pembagi berderajat
yang dapat difaktorkan maka sisanya berderajat
.
Contoh, polinominal  dibagi dengan
dibagi dengan  memiliki sisa (S) berikut
memiliki sisa (S) berikut
Teorema Faktor
Misalkan  adalah sebuah suku banyak dengan
adalah sebuah suku banyak dengan  adalah faktornya jika dan hanya jika
adalah faktornya jika dan hanya jika 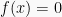 . Teorema faktor dapat dibaca sebagai berikut:
. Teorema faktor dapat dibaca sebagai berikut:
- Jika
faktor dari
, maka
.
- Jika
, maka
merupakan faktor dari
.
Contoh, menentukan faktor-faktor dari  . Konstanta
. Konstanta  memiliki faktor-faktor yang terdiri dari
memiliki faktor-faktor yang terdiri dari 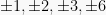 . Dengan metode bagan di atas atau metode substitusi bisa diketahui nilai agar
. Dengan metode bagan di atas atau metode substitusi bisa diketahui nilai agar 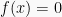 .
.
Sehingga faktor-faktornya adalah  ,
, 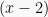 , dan
, dan  .
.
AKAR-AKAR PERSAMAAN SUKU BANYAK
Jika  dengan p≠0 adalah nilai nol dari f(x) maka p adalah pembagi
dengan p≠0 adalah nilai nol dari f(x) maka p adalah pembagi 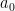 .
.
Jika  memiliki akar
memiliki akar  (pecahan murni) dengan
(pecahan murni) dengan 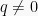 , maka p adalah pembagi
, maka p adalah pembagi 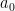 dan q adalah pembagi
dan q adalah pembagi 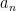 .
.
Sifat-sifat akar suku banyak:
Jika 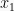 dan
dan 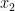 adalah akar persamaan
adalah akar persamaan 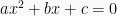 , maka
, maka
2. Persamaan pangkat tiga
Jika 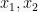 dan
dan 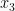 adalah akar persamaan
adalah akar persamaan 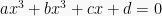 , maka:
, maka:
3. Persamaan pangkat empat
Jika 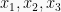 dan
dan  adalah akar persamaan
adalah akar persamaan  , maka:
, maka:
CONTOH SOAL SUKU BANYAK DAN PEMBAHASAN
Contoh Soal 1: Teorema Sisa
Suku banyak  dan
dan  dibagi dengan
dibagi dengan 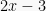 masing-masing menghasilkan sisa yang sama. Tentukan nilai a.
masing-masing menghasilkan sisa yang sama. Tentukan nilai a.
Pembahasan
Contoh Soal 2: Teorema Faktor
Tentukan nilai a dan b jika  habis dibagi
habis dibagi  .
.
Pembahasan:
Disubstitusi kedalam  menjadi :
menjadi :
Dari persamaan (1) dan (2) diperoleh:

Contoh Soal 3: Akar-akar Persamaan Suku Banyak
Diberikan persamaan 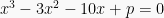 dengan akar-akarnya
dengan akar-akarnya 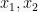 dan
dan
Pembahasan
Maka:
Kemudian disubstitusi dalam persamaan suku banyak:
Kemudian persamaan menjadi:
Jika dibagi  menjadi:
menjadi:

Sehingga:
Tidak ada komentar:
Posting Komentar