Persamaan Trigonometri
Persamaan trigonometri adalah persamaan yang mengandung perbandingan antara sudut trigonometri dalam bentuk x. Penyelesaian persamaan ini dengan cara mencari seluruh nilai sudut-sudut x, sehingga persamaan tersebut bernilai benar untuk daerah asal tertentu.
Penyelesaian persamaan trigonometri dalam bentuk derajat yang berada pada rentang  sampai dengan
sampai dengan  atau dalam bentuk radian yang berada pada rentang 0 sampai dengan 2π.
atau dalam bentuk radian yang berada pada rentang 0 sampai dengan 2π.
Rumus untuk menyelesaikan persamaan trigonometri sebagai berikut:
1. Sinus
Jika  dengan p dan a dalah konstanta, maka
dengan p dan a dalah konstanta, maka
- Dalam bentuk derajat:
Sebagai contoh:
Maka:
Menentukan himpunan penyelesaian umumnya yaitu:
k = 0  = 60 atau
= 60 atau 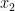 = 0
= 0
k = 1  = 180 atau
= 180 atau 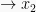 = 120
= 120
k = 2  = 300 atau
= 300 atau 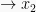 = 240
= 240
k = 3 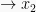 = 360
= 360
Jadi, himpunan penyelesaian umumnya adalah:
(0, 60, 120, 180, 240, 300, 360)
- Dalam bentuk radian:
Sebagai contoh:
Maka:
Menentukan himpunan penyelesaian umumnya yaitu:
k = 1  atau
atau 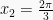
k = 2  atau
atau 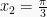
k = 3 
jadi, himpunan penyelesaian umumnya adalah:
2. Cosinus
Jika 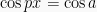 dengan p dan α adalah konstanta, maka:
dengan p dan α adalah konstanta, maka:
- Dalam bentuk derajat:
Sebagai contoh:
Maka:
Sehingga:
Diperoleh:
Menentukan himpunan penyelesaian umumnya yaitu:
Jadi, himpunan penyelesaian umumnya adalah:
- Dalam bentuk radian:
Sebagai contoh:
Maka:
Sehingga:
Diperoleh:
Menentukan himpunan penyelesaian umumnya yaitu:
jadi, himpunan penyelesaian umumnya adalah:
3. Tangen
Jika 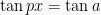 dengan p dan a adalah konstanta, maka
dengan p dan a adalah konstanta, maka
- Dalam bentuk derajat:
Sebagai contoh:
Maka:
Sehingga:
Menentukan himpunan penyelesaian umumnya yaitu:
Jadi, himpunan penyelesaian umumnya adalah:
- Dalam bentuk radian:
Menentukan himpunan penyelesaian umumnya yaitu:
Jadi, himpunan penyelesaian umumnya adalah:
PENYELESAIAN PERSAMAAN TRIGONOMETRI
Persamaan trigonometri dapat memuat jumlah atau selisih dari sinus atau kosinus. Untuk penyelesaiaannya dapat diubah menjadi bentuk persamaan yang memuat perkalian sinus atau kosinus. Begitu juga jika dihadapkan dengan kasus sebaliknya.
Persamaan trigonometri untuk beberapa kasus dapat dirubah menjadi persamaan kuadrat yang memuat sinus, kosinus, atau tangen. Penyelesaiannya didapat dengan metode faktorisasi.
Ada persamaan trigonometri dalam bentuk  yang dapat diselesaikan dengan cara berikut:
yang dapat diselesaikan dengan cara berikut:
Misalkan  , maka:
, maka:
Karena  , maka
, maka
Sebagai contoh:
Maka:
Sehingga:
Sehingga,
CONTOH SOAL PERSAMAAN TRIGONOMETRI DAN PEMBAHASAN
Contoh Soal 1
Tentukan himpunan penyelesaian dari persamaan:
Pembahasaan:
Sehingga,
Atau,
Himpunannya,
Himpunan penyelesaiannya adalah 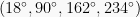
Contoh Soal 2
Tentukan himpunan penyelesaian dari persamaan:
Pembahasan
Dibuat kedalam bentuk
Dengan
Menjadikan
Sehingga
atau
Himpunannya,
Himpunan penyelesaiannya adalah:
Contoh Soal 3
Tentukan himpunan penyelesaian dari persamaan trigonometri:
Pembahasan:
Didapat,
Akar 1:
Akar 2:
Sehingga,
Atau,
Himpunannya,
Himpunan penyelesaiannya adalah:
Tidak ada komentar:
Posting Komentar